ANEJO 2. MÉTODO DEL MODO FUNDAMENTAL

(Formato PDF)

(Publicación con comentarios (Formato PDF))

A2.1. Condiciones generales

El método del modo fundamental es un método estático equivalente al modal espectral, cuya utilización sólo es válida cuando el comportamiento dinámico de la estructura pueda analizarse con suficiente precisión mediante un modelo dinámico de un sólo grado de libertad. Se puede considerar que esto se cumple en el caso de puentes de tablero sustentado por pilas verticales, siempre que se verifiquen además las condiciones siguientes:

• a) Para el cálculo en la dirección longitudinal, el tablero es continuo y aproximadamente recto, y la masa de todas las pilas es inferior a 1/5 de la masa del tablero.
• b) Para el cálculo en la dirección transversal, además de cumplirse las condiciones indicadas en a), la distribución de masa y rigidez del puente es aproximadamente simétrica alrededor del centro del tablero, es decir, la distancia, e₀, entre el centro de rigidez de los elementos de sustentación y el centro de masa del tablero no supera el 5% de la longitud del mismo.
• c) En el caso de pilas que soporten vanos isostáticos, la masa total de cada pila es inferior a 1/5 de la masa de la parte del tablero soportado por esa pila.

Se considerarán independientemente las componentes longitudinal, transversal y vertical de la acción sísmica. Para cada dirección, se determinará la fuerza estática equivalente que actúa sobre el tablero. La fuerza estática equivalente se obtendrá a partir de las fuerzas de inercia correspondientes al modo fundamental y al periodo natural de la estructura en la dirección considerada, obtenidas utilizando la ordenada correspondiente del espectro de cálculo.

Los efectos correspondientes a cada dirección se combinarán de acuerdo con las indicaciones recogidas el apartado 4.2.4.3 del articulado, de la misma forma que en el caso del cálculo modal espectral

En función de las características específicas de cada puente, el método del modo fundamental se aplica utilizando uno de los tres modelos simplificados que se exponen a continuación:

• Modelo de tablero rígido.
• Modelo de tablero flexible.
• Modelo de pila aislada

A2.2. Modelo de tablero rígido

Este modelo podrá aplicarse cuando, bajo la acción sísmica, la deformación del tablero en un plano horizontal sea despreciable en comparación con los desplazamientos de las pilas más los aparatos de apoyo.

Se puede suponer que esta condición que se cumple en los casos siguientes:

• En la dirección longitudinal, en puentes aproximadamente rectos con tablero continuo.
• En la dirección transversal si:

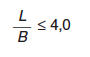donde:

• L Longitud del tablero continuo.
• B Anchura total del tablero.

o, en general, si se cumple la condición siguiente:

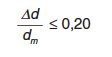donde Δd y d_m son, respectivamente, la máxima diferencia y el valor medio de los desplazamientos de las pilas más los aparatos de apoyo, en la dirección transversal, bajo la acción sísmica en esa dirección.

En puentes con tablero rígido, los efectos sísmicos se podrán calcular aplicando sobre el tablero una fuerza estática equivalente dada por la expresión siguiente:

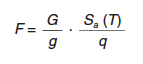donde:

• F Fuerza estática equivalente.
• G Peso total efectivo, que debe incluir el del tablero, el de la sobrecarga concomitante con el sismo y el de la mitad superior de las pilas.
• g Aceleración de la gravedad.
• q Factor de comportamiento, según el apartado 4.2.2 del articulado.
• S_a(T) Valor del espectro de aceleraciones en la dirección considerada, según el apartado 3.5.1 del articulado, correspondiente al periodo fundamental T del puente, estimado con la expresión: siendo K la rigidez del sistema, obtenida como suma de las rigideces de las pilas, en la dirección considerada

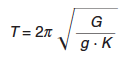La fuerza F se deberá repartir a lo largo del tablero de forma proporcional a la distribución de las masas efectivas.

El efecto de guiñada del tablero (ver figura C.4.6 del articulado) puede asimilarse a la acción de un momento torsor M_t de eje vertical:

donde:

• F Fuerza estática equivalente en dirección transversal.
• e Excentricidad de cálculo, de valor: e₀ Excentricidad teórica longitudinal, según el apartado A1.1.b).
• e_a Excentricidad accidental, de valor e_a = 0,05 L.
• L Longitud del tablero.

A2.3. Modelo de tablero flexible

Este modelo sólo será de aplicación si la diferencia máxima entre las luces de los vanos que componen el puente no supera el 20%.

En su aplicación se supone que la mayor parte de la respuesta de la estructura corresponde a una distribución de desplazamientos tipo, d, que, para cada una de las tres direcciones, se pueden obtener mediante la aplicación de las siguientes cargas estáticas de proyecto: fuerza de frenado para la dirección longitudinal, fuerza de viento para la transversal y peso propio para la vertical.

Para cada componente de la acción sísmica, se obtendrá un sistema de fuerzas equivalentes en esa dirección, actuando sobre cada nudo i de los N en que se haya discretizado la estructura, según la siguiente expresión:

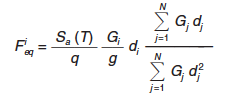donde:

Fⁱ_eq Fuerza estática equivalente en el nudo i.

S_a(T) Valor del espectro de aceleraciones en la dirección considerada, según el apartado 3.5.1 del articulado, correspondiente al periodo T asociado a los desplazamientos tipo, que se puede estimar con la expresión:

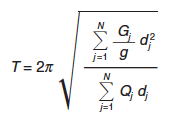siendo Q_j la carga concentrada en el nudo j utilizada para el cálculo de los desplazamientos tipo d_j.

• q Factor de comportamiento, según el apartado 4.2.2 del articulado.
• G_i Peso concentrado en el nudo i.
• g Aceleración de la gravedad.
• di Desplazamiento tipo del nudo i.

El efecto de guiñada del tablero (ver figura C.4.6 del articulado) puede asimilarse a la acción de un momento torsor M_t de eje vertical igual al definido para el caso de tablero rígido. El momento M_t puede repartirse entre los elementos de apoyo usando la hipótesis de tablero rígido.

A2.4. Modelo de pila aislada

En los casos en que la acción sísmica sea soportada básicamente por las pilas y de forma independiente por cada una de ellas, sin que exista una interacción importante con las adyacentes, el valor de la fuerza estática equivalente actuante al nivel del tablero podrá obtenerse de la expresión siguiente:

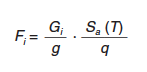donde:

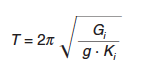• F_i Fuerza estática equivalente correspondiente a la pila i.
• G_i Peso efectivo, que debe incluir el de la parte del tablero soportado por la pila i, el de la sobrecarga correspondiente concomitante con el sismo y el de la mitad superior de la pila i.
• g Aceleración de la gravedad.
• q Factor de comportamiento, según el apartado 4.2.2 del articulado.
• S_a(T) Valor del espectro de aceleraciones en la dirección considerada, según el apartado 3.5.1 del articulado, correspondiente al periodo T, obtenido de la forma siguiente: siendo K_i la rigidez de la pila i, en la dirección considerada.