
 |
 |
 |
(Publicación con comentarios (Formato PDF))
El método utilizado con mayor frecuencia para el dimensionamiento de muros de contención de tierras es el denominado pseudoestático, desarrollado inicialmente por Okabe (1926) y Mononobe (1929), que se basa en la generalización de los principios de la estática (equilibrios de fuerzas y momentos) a la situación sísmica, mediante la adición, a las fuerzas existentes en la situación estática, de fuerzas de inercia y sobreempujes, que son función de las características del sismo analizado.
En esta teoría se supone la condición activa en el tradós del muro y la pasiva en el intradós, frente a la parte enterrada del cimiento, así como un terreno puramente granular.
Según la teoría del equilibrio límite, los empujes activo EAE y pasivo EPE corresponden, en condiciones estáticas, a las expresiones:
 |
Figura A6.1
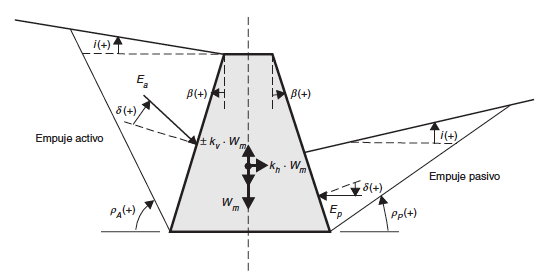 |
Cuando existan varios tipos de terreno en el trasdós, se puede utilizar la formulación expuesta con carácter general, adoptando valores medios del ángulo φ y del peso específico γ. Para el ángulo φ, se tomará la media ponderada de los ángulos de rozamiento interno de cada tipo de terreno en función de la longitud que cada uno de ellos intercepta en la línea base de la cuña de empuje en la sección transversal. Para el peso específico γ, se tomará la media ponderada de los pesos específicos de cada tipo de terreno en función de su área en la cuña de empuje contenida en la sección transversal.
Cuando sea necesario determinar la geometría de las cuñas activa y pasiva en condiciones dinámicas, se podrán adoptar las siguientes expresiones:
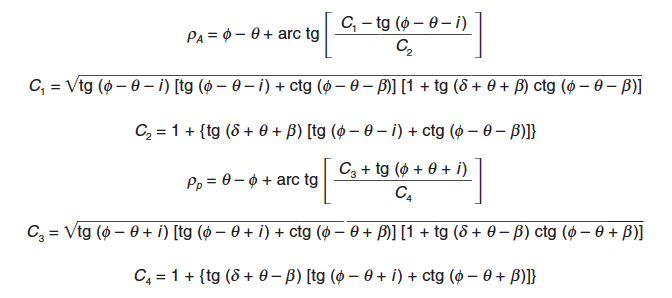 |
El método supone que los pesos de los elementos que intervienen en el problema se completan con fuerzas de inercia aplicadas en sus centros de gravedad, debiendo considerar la actuación de la aceleración sísmica vertical en sentido ascendente o descendente según resulte más desfavorable para el caso analizado. Se produce así una situación en que el ángulo de gravedad aparente con respecto a la vertical θ resulta:
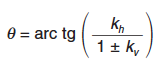 |
donde:
kh coeficiente sísmico horizontal para el que, en general, puede tomarse el siguiente valor:
Cuando pueda suponerse que no existen restricciones importantes al movimiento del estribo, y siempre que se pueda asegurar que no van a aparecer presiones intersticiales en el trasdós del mismo, podrán justificarse valores inferiores de este coeficiente. En cualquier caso, deberá cumplirse la condición siguiente:
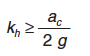 |
kv coeficiente sísmico vertical, para el que podrá tomarse el valor siguiente:
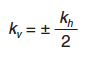 |
aunque en muchas comprobaciones podrá prescindirse de la acción sísmica vertical por tener poca influencia.
Cuando los muros superen los 10 m de altura, no serán de aplicación directa los valores anteriores de los coeficientes sísmicos, sino que éstos deberán determinarse para cada caso concreto mediante un estudio específico que tenga en cuenta la propagación vertical de las ondas sísmicas y los valores de pico de la aceleración horizontal obtenidos a diferentes alturas del muro.
La consideración del ángulo de gravedad aparente θ implica que, en condiciones dinámicas, las fórmulas de los empujes activo EAD y pasivo EPD resulten:
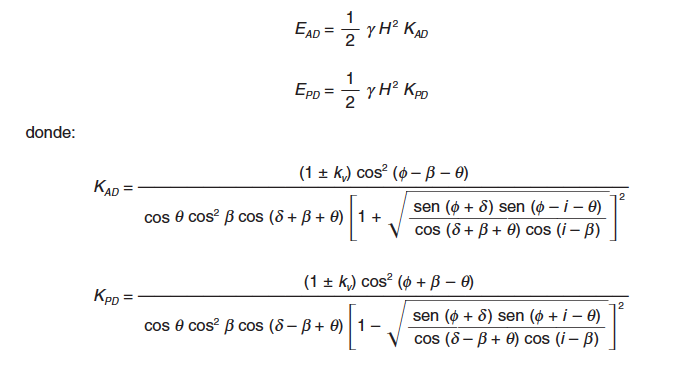 |
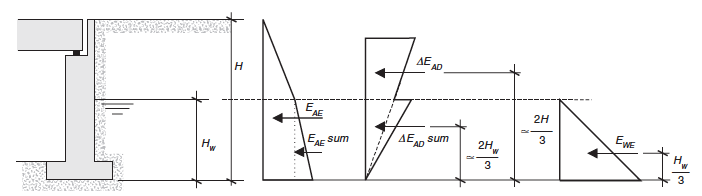
Respecto al punto de aplicación de los empujes, en el caso estático activo se admite un diagrama triangular de presiones con valor máximo en la base, mientras que en el dinámico la teoría empleada no permite su localización exacta. A efectos prácticos, puede considerarse aplicado a una altura de aproximadamente 2H/3, siguiendo una distribución triangular invertida respecto a la del caso estático activo.
Por ello se recomienda la utilización del esquema de la figura A6.2, en la que el empuje activo total se obtiene como suma del estático EAE y de un incremento dinámico ΔEAD, definido como:
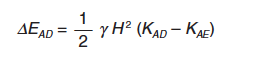 |
En consecuencia:
Figura A6.2
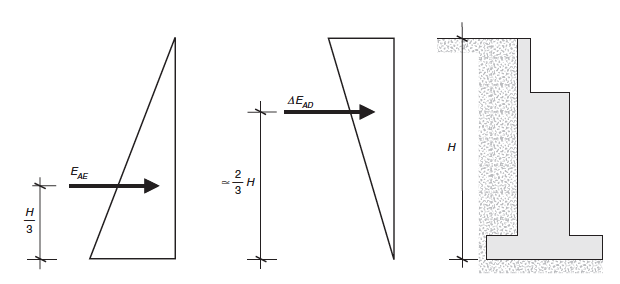 |
En los suelos sumergidos, en que pueda considerarse que el agua intersticial vibra junto con el esqueleto sólido, el valor de θ en los coeficientes de empuje anteriores debe sustituirse por el de θs, que se define como:
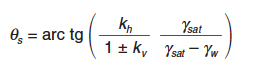 |
donde:
γsat Peso específico del suelo saturado.
γw Peso específico del agua, para el que podrá tomarse el valor γw = 9800 N/m3.
Simultáneamente, al calcular el empuje de las tierras debe utilizarse el peso específico sumergido (γsum = γsat – γw).
En los suelos sumergidos de alta permeabilidad, en los que pueda suponerse que la vibración del agua y la del esqueleto sólido son independientes, debe sustituirse el ángulo θ por θd:
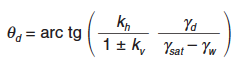 |
En los casos habituales de rellenos de trasdós, se considerará que la vibración de agua y esqueleto sólido es conjunta.
Simultáneamente, al calcular el empuje de las tierras debe utilizarse el peso específico del suelo seco γd.
Además, en este caso, al empuje estático del agua debe añadirse el hidrodinámico, de valor:
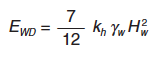 |
En el caso de trasdoses parcialmente sumergidos (figura A6.3), se precisan dos valores del coeficiente de empuje dinámico: el correspondiente al terreno de la parte superior
Figura A6.3
 |
KAD, donde se utiliza el valor del ángulo θ, y el correspondiente al terreno de la parte inferior KADsum, donde, se utiliza normalmente el ángulo θs y el peso específico sumergido.
En este caso el empuje activo total resulta:
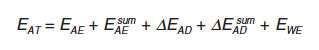 |
donde:
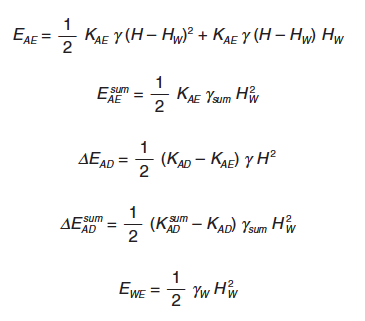 |
En el caso de suelos totalmente sumergidos con una lámina de agua libre superior, debe añadirse el empuje hidrodinámico EWD, aplicado a una altura 0,4(Hw-h) medida desde el lecho, según se indica en la figura A6.4.
Figura A6.4
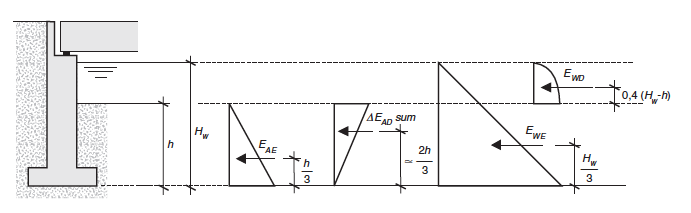 |
El empuje activo total resulta:
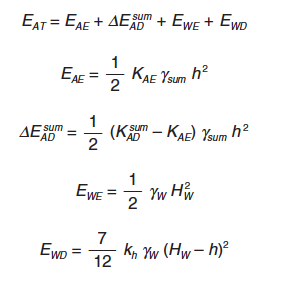 |
A las acciones anteriores habrá de añadirse en todo caso la subpresión bajo el plano del cimiento, cuando sea previsible su existencia.
 |
 |
 |