CAPÍTULO XII ELEMENTOS ESTRUCTURALES
Artículo 52.º Elementos estructurales de hormigón en masa
52.1. Ámbito de aplicación
Se considerarán
elementos estructurales de hormigón en masa los construidos con hormigón sin armaduras,
y los que tienen armaduras sólo para reducir los efectos de la fisuración, generalmente
en forma de mallas junto a los paramentos.
No es aplicable este
capítulo, salvo con carácter subsidiario, a aquellos elementos estructurales de
hormigón en masa que tengan su normativa específica.
52.2.Hormigones utilizables
Para elementos de
hormigón en masa se podrán utilizar los hormigones definidos en 39.2.
52.3. Acciones de cálculo
Las acciones de cálculo
combinadas aplicables en los Estados Límite Últimos son las indicadas en el Artículo 13.º
52.4. Cálculo de secciones a compresión
En una sección de un
elemento de hormigón en masa en la que actúa solamente un esfuerzo normal de
compresión, con valor de cálculo Nd (positivo), aplicado en un punto G, con
excentricidad de componentes (ex, ey), respecto a un sistema de ejes
cobaricéntricos (caso a; Figura 52.4.a), se considerará Nd aplicado en el
punto virtual G1(e1x, e1y), que será el que resulte más
desfavorable de los dos siguientes:
G1x(ex+ exa, ey) ó
G1y(ex, ey+eya)
donde:
- hx y hy Dimensiones máximas en dichas direcciones.
- exa = 0,05hx no menor de 2cm
- eya = 0,05hy no menor de 2 cm
Figura 52.4.a
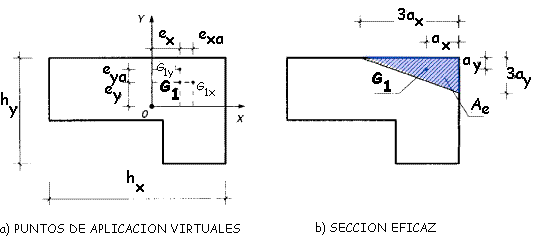
La tensión resultante sd se calcula admitiendo una
distribución uniforme de tensiones en una parte de la sección, denominada sección
eficaz, de área Ae (caso b; figura 52.4.a), delimitada por una recta secante y
cuyo baricentro coincide con el punto de aplicación virtual G del esfuerzo normal y
considerando inactiva el resto de la sección.
La condición de
seguridad es:
Nd/Ae
£ 0,85fcd
52.5. cálculo de secciones a compresión y esfuerzo cortante
En una sección de un
elemento de hormigón en masa en la que actúa un esfuerzo oblicuo de compresión, con
componentes en valor de cálculo Nd y Vd (positivas) aplicado en el
punto G, se determina el punto de aplicación virtual G1, y el área eficaz Ae,
como en 52.4. Las condiciones de seguridad son:
Nd/Ae
£ 0,85fcd
Vd/Ae
£ 0,85fct,d
52.6. Consideración de la esbeltez
En un elemento de
hormigón en masa sometido a compresión, con o sin esfuerzo cortante, los efectos de
primer orden que produce Nd se incrementan con efectos de segundo orden a causa
de su esbeltez (52.6.3). Para tenerlos en cuenta se considerará Nd actuando en
un punto G2 que resulta de desplazar G1 (52.4) una excentricidad
ficticia definida en 52.6.4.
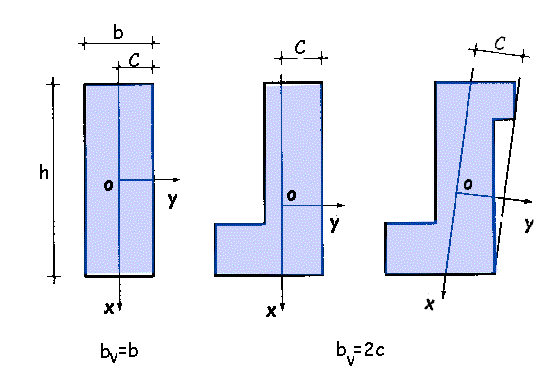
52.6.1. Anchura virtual
Como anchura virtual bv
de la sección de un elemento se tomará: bv = 2c, siendo c la mínima
distancia del baricentro de la sección (figura 52.6.1) a una recta rasante a su
perímetro.
Figura 52.6.1
52.6.2. Longitud de pandeo
Como longitud de pandeo
lo de un elemento se toma: lo=bl siendo l la altura del elemento entre base y coronación, y b=boz el
factor de esbeltez, con bo=1
en elementos con coronación arriostrada horizontalmente y bo=2 en elementos con coronación sin arriostrar. El factor
z tiene en cuenta el efecto
del arriostramiento por muros transversales, siendo:
z=(5/4l)1/2
no mayor de 1
donde:
- s Separación entre muros de arriostramiento.
En pilares u otros
elementos exentos se toma z=1.
52.6.3. Esbeltez
La esbeltez l de un elemento de hormigón en masa se
determina por la expresión:
l=lo/bv
52.6.4. Excentricidad ficticia
El efecto de pandeo de
un elemento con esbeltez l se
considera equivalente al que se produce por la adición de una excentricidad ficticia ea
en dirección del eje y paralelo a la anchura virtual bv de la sección de
valor:
ea= (15/Ec)(bv +e1)l2
donde:
- Ec Módulo instantáneo de deformación secante del hormigón en N/mm2
a la edad de 28 días (39.6).
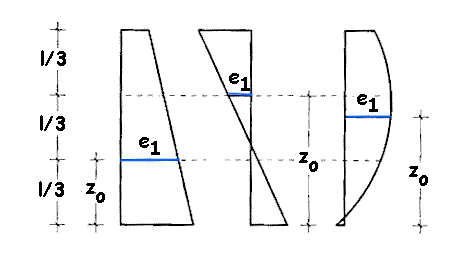
- e1 Excentricidad determinante (figura 52.6.4), que vale:
- Elementos con coronación arriostrada horizontalmente: el máximo valor de e1y
en la abscisa z0.
1/3 £ z0 £ 2l/3
- Elementos con coronación no arriostrada: el valor de e1y en la base.
El elemento se calcula
en la abscisa z0 con excentricidad de componentes (e1x, e1+ea)
y en cada extremo con su correspondiente excentricidad (e1x, e1y).
Figura 52.6.4