Artículo 8.º Sobreanchos en las curvas.-
Los vehículos, cuando
recorren una curva, en razón a la rigidez del chasis y a la dificultad que siempre
encierra el tenerse que inscribir a una determinada velocidad en la trayectoria que se
siga, necesitan un espacio mayor del que constituye su vía, o sea del ancho definido por
la separación de sus ruedas; cuyo mayor espacio es de tanta más importancia cuanto mayor
sea la longitud del vehículo y cuanto menor sea el radio de la curva.
En dicho caso, la
dirección del eje-motor coincide sensiblemente con el radio de la curva, describiendo, en
cambio, las ruedas delanteras una curva de radio superior; la diferencia entre los dos
radios mencionados nos da el sobreancho necesario para una vía, el cual ha de ser
considerado como mínimo, por cuanto obedece únicamente a la consideración estática,
una de las dos anteriormente aludidas.
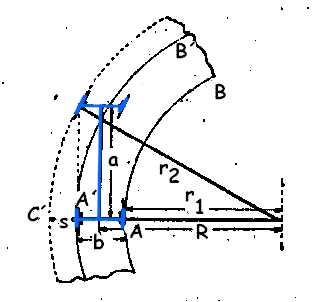
Consecuentemente, en el
caso de la figura y en el supuesto de que el eje de la vía corresponde al del camino, el
sobreancho vendrá determinado por:
- A´C´= s = r2-(R+b/2)
- r2= [ (R+b/2)2+a2]1/2
- s = [ (R+b/2)2+a2]1/2- (R+b/2)
Particularizando la
presente fórmula para él caso de los mayores autómnibus conocidos, que tiene un ancho
de vía de b = 1,90 metros y una batalla a = 6,00 metros, y para distintos radios, tenemos
los siguientes resultados para una, dos y tres vías:
| R=10,00m |
s=1,49m |
s=2,98m |
s=4,47m |
| R=20,00m |
s=0,84m |
s=1,68m |
s=2,52m |
| R=30,00m |
s=0,59m |
s=1,18m |
s=1,77m |
| R=45,00m |
s=0,39m |
s=0,78m |
s=1,17m |
| R=60,00m |
s=0,29m |
s=0,58m |
s=0,87m |
| R=100,00m |
s=0,18m |
s=0,36m |
s=0,54m |
| R=200,00m |
s=0,09m |
s=0,18m |
s=0,27m |
