Figura 38.2 Diagrama característico tensión-deformación para armaduras pasivas
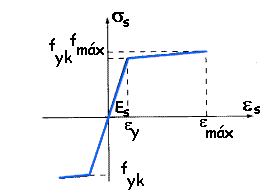
fyd=fyk/
gs siendo el límite elástico característico y gs el coeficiente parcial de seguridad definido en el Articulo 15.ºEn el caso de emplear un nivel reducido de control para el acero (90.2), deberá tomarse como resistencia de cálculo del acero el valor:
fyd=0,75·fyk/gs
Las expresiones indicadas son válidas tanto para tracción como para compresión.
Cuando en una misma sección coincidan aceros con diferente límite elástico, cada uno se considerará en el cálculo con su diagrama correspondiente.
El diagrama tensión-deformación de cálculo del acero para armaduras pasivas (en tracción o en compresión) se deduce del diagrama característico mediante una afinidad oblicua, paralela a la recta de Hooke, de razón 1/gs.
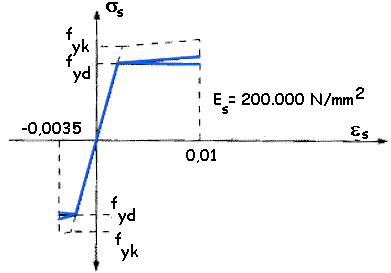
Cuando se utiliza el diagrama de la figura 38.2, se obtiene el diagrama de cálculo de la figura 38.4 en la que se observa que se puede considerar a partir de fyd una segunda rama con pendiente positiva, obtenida mediante afinidad oblicua a partir del diagrama característico, o bien una segunda rama horizontal, siendo esto último suficientemente preciso en general.
Se admite el empleo de otros diagramas de cálculo simplificados, siempre que su uso conduzca a resultados que estén suficientemente avalados por la experiencia.
Figura 38.4. Diagrama tensión-deformación de cálculo para armaduras pasivas
Como diagrama tensión-deformación característico del acero para armaduras activas (alambre, barra o cordón) puede adoptarse el que establezca su fabricante hasta la deformación ep= 0,010, como mínimo, y tal que, para una deformación dada las tensiones sean superadas en el 95% de los casos.
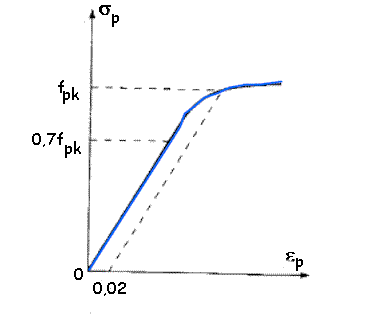
Si no se dispone de este diagrama garantizado, puede utilizarse el representado en la figura 38.5. Este diagrama consta de un primer tramo recto de pendiente Ep y un segundo tramo curvo, a partir de 0,7fpk y, definido por la siguiente expresión:
ep=sp/Ep +0,823(sp/fpk- 0,7)5 para sp³07·fpk
siendo Ep el módulo de deformación longitudinal definido en 38.8.
Figura 38.5. Diagrama tensión-deformación característico para armaduras pasivas
Como resistencia de cálculo del acero para armaduras activas, se tomará:
fpd=fpk/gs
siendo fpd el valor del límite elástico característico y gs el coeficiente parcial de seguridad del acero dado en el Artículo 15.º.
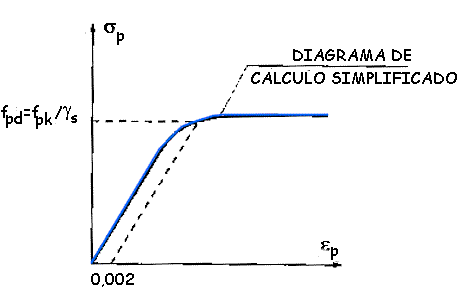
El diagrama tensión-deformación de cálculo del acero para armaduras activas, se deducirá del correspondiente diagrama característico, mediante una afinidad oblicua, paralela a la recta de Hooke, de razón 1/gs (ver figura 38.7.a).
Como simplificación, a partir de fpd se podrá tomar sp=fpd (ver figura 38.7.b).
Figura 38.7a. Diagrama tensión-deformación de cálculo para armaduras activas
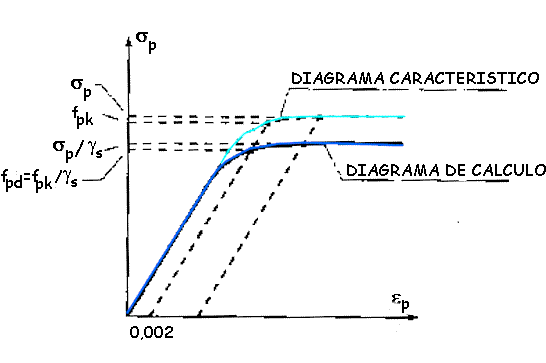
Figura 38.7.b. Diagrama tensión-deformación de cálculo para armaduras activas
Como módulo de deformación longitudinal del acero de las armaduras constituidas por alambres o barras se adoptará, salvo justificación experimental, el valor Ep= 200.000 N/mm2.
En los cordones, se pueden adoptar como valores noval y reiterativo los que establezca el fabricante o se determinen experimentalmente. En el diagrama característico (véase 38.5) debe tomarse el valor del módulo reiterativo. Si no existen valores experimentales anteriores al proyecto puede adoptarse el valor Ep = 190.000 N/mm2.
Para la comprobación de alargamiento durante el tesado se requiere utilizar el valor del módulo noval determinado experimentalmente.
La relajación r del acero a longitud constante, para una tensión inicial spi=afmáx estando la fracción a comprendida entre 0,5 y 0,8 y para un tiempo t, puede estimarse con la siguiente expresión:
log r= log (Dsp/spi)=K1+K2log t
donde:
Figura 38.9
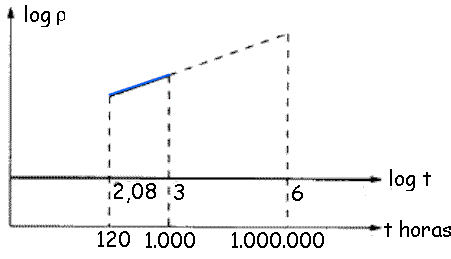
El fabricante del acero suministrará los valores de la relajación a 120 h y a 1.000 h, para tensiones iniciales de 0,6; 0,7 y 0,8 de fmáx a temperaturas de 20º±1ºC y garantizará el valor a 1.000 h para a = 0,7.
Con estos valores de relajación pueden obtenerse los coeficientes K1 y K2 para a=0,6; 0,7 y 0,8.
Para obtener la relajación con otro valor de a puede interpolarse linealmente admitiendo para a=0,5; r=0.
Como valor final rf se tomará el que resulte para la vida estimada de la obra expresada en horas, o 1.000.000 de horas a falta de este dato.
La variación de tensión máxima, debida a la carga de fatiga, debe ser inferior a los valores del límite de fatiga indicados en la tabla 38.10.
TABLA 38.10 Límite de fatiga para armaduras pasivas y activas
| TIPO DE ACERO | Límite de fatiga DsD(N/mm2) | |
| Adherencia directa | Adherencia dentro de vainas de acero |
|
| Armaduras pasivas - Barras - Mallas electrosoldadas |
. 150 100 |
. - - |
| Armaduras activa - Alambres - Cordones constituidos por 7 alambres - Barras de pretensado |
. 150 150 - |
. 100 100 100 |
En el caso de barras dobladas, a falta de resultados experimentales específicos y representativos, el límite de fatiga indicado en la tabla 38.10 deberá disminuirse según el siguiente criterio:
DsD,red=(1-3d/D)DsD
donde:
En el caso de estribos verticales de diámetro menor o igual a 10 mm, no será necesaria ninguna reducción del límite de fatiga.
Los dispositivos de anclaje y empalme se situarán, en la medida de lo posible, en secciones donde sea mínima la variación de tensiones.
En general, el límite de fatiga de este tipo de elementos es inferior al de las armaduras y deberá ser suministrado por el fabricante después de la realización de ensayos específicos y representativos.