Este articulo concierne a la comprobación de soportes aislados, estructuras aporticadas y estructuras reticulares en general, en que los efectos de segundo orden no pueden ser despreciados.

La aplicación de este artículo está limitada a los casos en que pueden despreciarse los efectos de torsión.

Esta Instrucción no cubre los casos en que la esbeltez mecánica l de los soportes (ver definición en 43.1.2) es superior a 200.

A los efectos de aplicación de este Artículo 43.º se denominan:

• Estructuras intraslacionales aquellas cuyos nudos, bajo solicitaciones de cálculo, presentan desplazamientos transversales cuyos efectos pueden ser despreciados desde el punto de vista de la estabilidad del conjunto.
• Estructuras traslacionales aquellas cuyos nudos, bajo solicitaciones de cálculo, presentan desplazamientos transversales cuyos efectos no pueden ser despreciados desde el punto de vista de la estabilidad del conjunto.
• Soportes aislados, los soportes isostáticos, o los de pórticos en los que puede suponerse que la posición de los puntos donde se anula el momento de segundo orden no varía con el valor de la carga.
• Esbeltez mecánica de un soporte de sección constante, el cociente entre la longitud de pandeo l_o del soporte (distancia entre puntos de inflexión de la deformada) y el radio de giro i de la sección bruta de hormigón en la dirección considerada.
• Esbeltez geométrica de un soporte de sección constante, el cociente entre la longitud de pandeo l_o del soporte y la dimensión (b ó h) de la sección que es paralela al plano de pandeo.

La comprobación general de una estructura, teniendo en cuenta las no linealidades geométrica y mecánica, puede realizarse de acuerdo con los principios generales indicados en 21.3.4 y 21.3.5. Con esta comprobación se justifica que la estructura, para las distintas combinaciones de acciones posibles, no presenta condiciones de inestabilidad global ni local, a nivel de sus elementos constitutivos, ni resulta sobrepasada la capacidad resistente de las distintas secciones de dichos elementos.

Deben considerarse en el cálculo las incertidumbres asociadas a la predicción de los efectos de segundo orden y, en particular, los errores de dimensión e incertidumbres en la posición y línea de acción de las cargas axiles.

En las estructuras intraslacionales, el cálculo global de esfuerzos podrá hacerse según la teoría de primer orden. A partir de los esfuerzos así obtenidos, se efectuará una comprobación de los efectos de segundo orden de cada soporte considerado aisladamente, de acuerdo con 43.5.

Las estructuras traslacionales serán objeto de una comprobación de estabilidad de acuerdo con las bases generales de 43.2.

Para soportes con esbeltez mecánica comprendida entre 100 y 200 se aplicará el método general establecido en 43.5.1.

Para soportes con esbeltez mecánica comprendida entre 35 y 100 puede aplicarse el método aproximado de 43.5.2 ó 43.5.3.

Para soportes con esbeltez mecánica inferior a 35 pueden despreciarse los efectos de segundo orden y, en consecuencia, no efectuar comprobación alguna en relación con el Estado Límite de Inestabilidad.

En general la comprobación de soportes aislados se llevará a cabo de acuerdo con las bases de 43.2.

Para soportes de sección y armadura constante deberá dimensionarse la sección para una excentricidad total igual a la que se indica:

e_a=(1+0,12b)(e_y+e)[(h+20e_e)l₀²/(h+10e_e)50i_c]

• e_a Excentricidad ficticia utilizada para representar los efectos de segundo orden.
• e_e Excentricidad de cálculo de primer orden equivalente.
  • e_e= 0,6e₂ + 0,4e₁ no menor de 0,4e₂ para soportes intraslacionales;
  • e_e= e₂ para soportes traslacionales.
• e₂ Excentricidad de cálculo máxima de primer orden, tomada con signo positivo.
• e₁ Excentricidad de cálculo mínima de primer orden, tomada con el signo que le corresponda.
• l₀ Longitud de pandeo.
• i_c Radio de giro de la sección de hormigón en la dirección considerada.
• h Canto total de la sección de hormigón.
• e_y Deformación del acero para la tensión de cálculo f_yd, es decir,
      e_y = f_yd/E_s
• e Parámetro auxiliar para tener en cuenta los efectos de la fluencia:
  • e=0,003 cuando el axil cuasipermanente no supera el 70% del axil total.
  • e=0,004 cuando el axil cuasipermanente es mayor que el 70% del axil total.
• b Factor de armado.
      b= (d-d´)²/4i_s² siendo i_s el radio de giro de las armaduras. Los valores de b y de  i_s se recogen en la tabla 43.5.2 para las disposiciones de armaduras más frecuentes.

TABLA 43.5.2

Disposición de la armadura	is2	b
	1/4(d-d´)2	1,0
	1/12(d-d´)2	3,0
	1/6(d-d´)2	1,5

43.5.3. Método aproximado. Flexión compuesta esviada

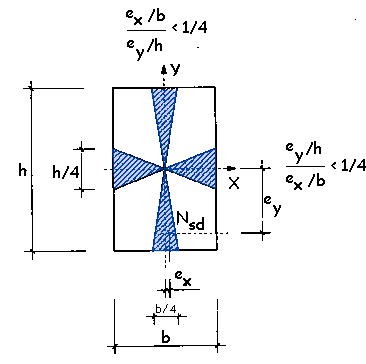
Para elementos de sección rectangular y armadura constante se podrá realizar una comprobación separada, según los dos planos principales de simetría, si la excentricidad del axil se sitúa en la zona rayada de la figura 43.5.3.a. Esta situación se produce si se cumple alguna de las dos condiciones indicadas en la figura 43.5.3.a, donde e_x y e_y son las excentricidades de cálculo en la dirección de los ejes x e y, respectivamente.

Figura 43.5.3.a

Cuando no se cumplen las condiciones anteriores, podrá comprobarse el soporte esbelto si se cumple la siguiente condición:

(M_xd/M_xu)+(M_yd/M_yu)£1

donde:

• M_xd Momento de cálculo, en la dirección x, en la sección crítica de comprobación, considerando los efectos de segundo orden.
• M_yd Momento de cálculo, en la dirección y, en la sección crítica de comprobación, considerando los efectos de segundo orden.
• M_xu Momento máximo, en la dirección x, resistido por la sección crítica.
• M_yu Momento máximo, en la dirección y, resistido por la sección crítica.