Artículo 44.º Estado Límite de Agotamiento frente a cortante
44.1. Consideraciones generales
Para el análisis de la
capacidad resistente de las estructuras de hormigón frente a esfuerzos cortantes, se
establece como método general de cálculo el de Bielas y Tirantes (Artículos 24.º y 40.º), que deberá utilizarse en todos
aquellos elementos estructurales o partes de los mismos que, presentando estados planos de
tensión o asimilables a tales, estén sometidos a solicitaciones tangentes según un
plano conocido y no correspondan a los casos particulares tratados de forma explícita en
esta Instrucción, tales como elementos lineales, placas y losas (44.2).
44.2. Resistencia a esfuerzo cortante de elementos lineales, placas y losas
Las prescripciones
incluidas en los diferentes subapartados son de aplicación exclusivamente a elementos
lineales sometidos a esfuerzos combinados de flexión, cortante y axil (compresión o
tracción) y a placas o losas trabajando fundamentalmente en una dirección.
A los efectos de este
artículo se consideran elementos lineales aquellos cuya distancia entre puntos de momento
nulo es igual o superior a dos veces su canto total y cuya anchura es igual o inferior a
cinco veces dicho canto, pudiendo ser su directriz recta o curva. Se denominan placas o
losas a los elementos superficiales planos, de sección llena o aligerada, cargados
normalmente a su plano medio.
44.2.1. Definición de la sección de cálculo
Para los cálculos
correspondientes al Estado Límite de Agotamiento por esfuerzo cortante, las secciones se
considerarán con sus dimensiones reales en la fase analizada. Excepto en los casos en que
se indique lo contrario, la sección resistente del hormigón se obtiene a partir de las
dimensiones reales de la pieza, cumpliendo los criterios indicados en 40.3.5.
44.2.2. Esfuerzo cortante efectivo
Las comprobaciones
relativas al Estado Límite de Agotamiento por esfuerzo cortante pueden llevarse a cabo a
partir del esfuerzo cortante efectivo Vrd dado por la siguiente expresión:
Vrd=Vd+Vpd+Vcd
donde:
- Vd Valor de cálculo del esfuerzo cortante producido por las acciones
exteriores.
- Vpd Valor de cálculo de la componente de la fuerza de pretensado paralela a
la sección en estudio.
- Vcd Valor de cálculo de la componente paralela a la sección de la
resultante de tensiones normales, tanto de compresión como de tracción, sobre las fibras
longitudinales de hormigón, en piezas de sección variable.
44.2.3. Comprobaciones que hay que realizar
El Estado Límite de
Agotamiento por esfuerzo cortante se puede alcanzar, ya sea por agotarse la resistencia a
compresión del alma, o por agotarse su resistencia a tracción. En consecuencia, es
necesario comprobar que se cumple simultáneamente:
£Vu1
Vrd£Vu2
donde:
- Vrd Esfuerzo cortante efectivo de cálculo definido en 44.2.2.
- Vu1 Esfuerzo cortante de agotamiento por compresión oblicua en el alma.
- Vu2 Esfuerzo cortante de agotamiento por tracción en el alma.
La comprobación del
agotamiento por compresión oblicua en el alma
Vrd £ Vu1 se realizará en el borde del apoyo y no en su eje.
En piezas sin armadura
de cortante no resulta necesaria la comprobación de agotamiento por compresión oblicua
en el alma.
La comprobación
correspondiente al agotamiento por tracción en el alma
Vrd £ Vu2 se efectúa para una sección situada a una distancia
de un canto útil del borde del apoyo directo.
44.2.3.1. Obtención de Vu1
El esfuerzo cortante de
agotamiento por compresión oblicua del alma se deduce de la siguiente expresión:
Vu1=K·f1cd·b0·d·[(cotg
q+cotga)/(1+cotg2q)]
donde:
- f1cd Resistencia a compresión del hormigón f1cd=0,60fcd
- b0 Anchura neta mínima del elemento, definida de acuerdo
con 40.3.5.
- K Coeficiente de reducción por efecto del esfuerzo axil
K=5/3(1+
s´cd/fcd)
no mayor de 1,00
donde:
s´cd tensión
axil efectiva en la sección (tracción positiva) s´cd=Nd/Ac
Nd Esfuerzo axil de cálculo (tracción positiva) incluyendo el pretensado con
su valor de cálculo
Ac Area total de la sección de hormigón
a Ángulo
de las armaduras con el eje de la pieza (figura 44.2.3.1 a).
q Ángulo
entre las bielas de compresión de hormigón y el eje de la pieza (figura 44.2.3.1 a). Se
adoptará un valor que cumpla: 0,5 < cotg q < 2,0
Figura 44.2.3.1.a
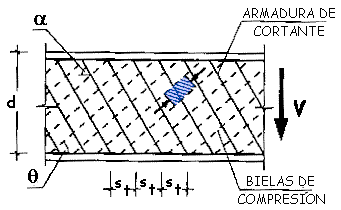
44.2.3.2. Obtención de Vu2
44.2.3.2.1. Piezas sin armadura de cortante
El esfuerzo cortante de
agotamiento por tracción en el alma vale
Vu2=[0,12·
x·(100·rl·fck)1/3-0,15s´cd]b0·d
con fck expresado en N/mm2,
donde:
x=1+(200/d)1/2
con d en mm
rl
Cuantía geométrica de la armadura longitudinal traccionada, pasiva y activa adherente,
anclada a una distancia igual o mayor que d a partir de la sección de estudio
rl=[As+Ap(fyp/fyd)]/b0·d
no mayor de 0,02
44.2.3.2.2. Piezas con armadura de cortante
El esfuerzo cortante de
agotamiento por tracción en el alma vale:
Vu2=Vcu+Vsu
donde:
- Vsu Contribución de la armadura transversal de alma a la resistencia a
esfuerzo cortante.
Vsu= z·sena(cotga+cotgq)SAafya,d donde:
- Aa Área por unidad de longitud de cada grupo de armaduras que forman
un ángulo a
con la directriz de la pieza (figura 44.2.3.1)
- fya,d Resistencia de cálculo de la armadura Aa (40.2)
ya,d = ssd
- Para armaduras activas fya,d = spd
- z Brazo mecánico. A falta de cálculos más precisos puede
adoptarse el valor aproximado z=0,9d.
Vcu contribución del hormigón a la resistencia a esfuerzo cortante
Vcu=[0,10·x·(100·rl·fck)1/3-0,15s´cd]b0·d·b con fck
expresado en N/mm2, donde:
- b= (2cotgq -1)/(2cotgqe-1) si 0,5
< cotgq
< cotgqe
- b= (cotgq -2)/(cotgqe-2) si cotgqe < cotgq < 2,0
- qe
Ángulo de referencia de inclinación de las fisuras, deducido de la expresión:
cotgqe=[f2ct,m-fct,m(sxd+syd)+sxd·syd]1/2/(fct,m-syd)
no menor de 0,5 ni mayor de 2,0
- fct,m Resistencia media a tracción del hormigón (39.1)
considerada como positiva.
- sxd,syd
Tensiones normales de cálculo, a nivel del centro de gravedad de la sección, paralelas a
la directriz de la pieza y al esfuerzo cortante Vd respectivamente. Las
tensiones sxd y
syd se obtendrán a
partir de las acciones de cálculo, incluido el pretensado, de acuerdo con la Teoría de
la Elasticidad y en el supuesto de hormigón no fisurado y considerando positivas las
tensiones de tracción.
44.2.3.3. Casos especiales de carga
Cuando se somete una
viga a una carga colgada, aplicada a un nivel tal que quede fuera de la cabeza de
compresión de la viga, se dispondrán las oportunas armaduras transversales, armaduras de
suspensión, convenientemente ancladas, para transferir el esfuerzo correspondiente a
aquella cabeza de compresión.
Por otra parte, en las
zonas extremas de las piezas pretensadas, y en especial en los casos de armaduras activas
pretesas ancladas por adherencia, será necesario estudiar el efecto de la introducción
progresiva de la fuerza de pretensado en la pieza, valorando esta fuerza en cada sección.
44.2.3.4. Disposiciones relativas a las armaduras
44.2.3.4.1. Armaduras transversales
La separación st
entre armaduras transversales (figura 44.2.3.1 a) deberá cumplir las condiciones
siguientes para asegurar un adecuado confinamiento del hormigón sometido a compresión
oblicua:
£ 0,80d no mayor de 300 mm si Vrd £ Vu1/5
st £ 0,60d no mayor de 300 mm si Vu1/5 < Vrd £ 2Vu1/3
st £ 0,30d no mayor de 200 mm si Vrd > 2Vu1/3
Si existe armadura de
compresión y se tiene en cuenta en el cálculo, los cercos o estribos cumplirán,
además, las prescripciones del Artículo 42.º.
Para un control eficaz,
en piezas lineales, de la fisuración inclinada de alma debida a solicitaciones
tangenciales, deberán respetarse las separaciones entre armaduras transversales indicadas
en 49.3.
En general, los
elementos lineales dispondrán de armadura transversal anclada de forma efectiva.
En todos los casos, se
prolongará la colocación de cercos o estribos en una longitud igual a medio canto de la
pieza, más allá de la sección en la que teóricamente dejen de ser necesarios. En el
caso de apoyos, los cercos o estribos se dispondrán hasta el borde de los mismos.
Las armaduras de
cortante deben formar con el eje de la viga un ángulo comprendido entre 45º y 90º,
inclinadas en el mismo sentido que la tensión principal de tracción producida por las
cargas exteriores, al nivel del centro de gravedad de la sección de la viga supuesta no
fisurada.
Las barras que
constituyen la armadura transversal pueden ser activas o pasivas, pudiendo disponerse
ambos tipos de forma aislada o en combinación.
La cuantía mínima de
tales armaduras debe ser tal que se cumpla la relación:
S(Aa·fya,d/sena) ³ 0,02·fcd·b0
Al menos un tercio de la
armadura necesaria por cortante, y en todo caso la cuantía mínima indicada, se
dispondrá en forma de estribos que formen un ángulo de 90º con el eje de la viga.
44.2.3.4.2. Armaduras longitudinales
Las armaduras
longitudinales de flexión deberán ser capaces de soportar un incremento de tracción
respecto a la producida por Md, igual a:
DT=Vrd·cotgq -Vsu/2(cotgq+cotga)
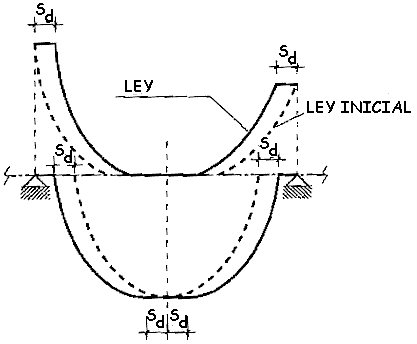
Esta prescripción se
cumple de forma automática decalando la ley de momentos de cálculo Md una
magnitud igual a:
Sd=z[cotgq -Vsu·(cotgq+cotga)/(2Vrd)]
en el sentido más desfavorable (figura 44.2.3.4.2).
Figura 44.2.3.4.2
En el caso de no existir
armadura de cortante, se tomará Vsu=0 en las expresiones
anteriores.
44.2.3.5. Rasante entre alas y alma de una viga
Para el cálculo de la
armadura de unión entre alas y alma de las cabezas de vigas en T, en I, en cajón o
similares, se empleará en general el método de Bielas y Tirantes (Artículo
40.º).
Para la determinación
del esfuerzo rasante puede suponerse una redistribución plástica en una zona de la viga
de longitud ar (figura 44.2.3.5.a).
Figura 44.2.3.5.a
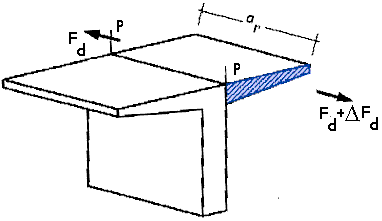
El esfuerzo rasante
medio por unidad de longitud que debe ser resistido será:
Sd=DFd/ar
donde:
- ar Longitud de redistribución plástica considerada La ley
de momentos en la longitud ar debe presentar variación
monótona creciente o decreciente. Al menos los puntos de cambio de signo de momento deben
adoptarse siempre como límites de zona ar.
- DFd
Es la variación en la distancia ar de la fuerza longitudinal
actuante en la sección del ala exterior al plano P.
En ausencia de cálculos más rigurosos deberá cumplirse:
Sd£Su1
Sd£Su2
donde:
- Su1 Esfuerzo rasante de
agotamiento por compresión oblicua en el plano P
Su1=0,5·f1cdh0
donde:
- f1cd Resistencia a compresión
del hormigón (40.3.2), de valor:
f1cd = 0,60fcd para alas
comprimidas;
f1cd= 0,40fcd para alas
traccionadas.
- h0 Espesor del ala de acuerdo con
40.3.5.
- Su2 Esfuerzo rasante de
agotamiento por tracción en el plano P.
Su2=Ssu
donde:
- Ssu Contribución de la armadura
perpendicular al plano P a la resistencia a esfuerzo rasante.
Ssu=Ap·fyp,d
- Ap Armadura por unidad de
longitud perpendicular al plano P (figuras 44.2.3.5.b y c).
- fyp,d Resistencia de cálculo de
la armadura Ap
fyp,d = ssd
para armaduras pasivas;
fyp,d= spd para armaduras activas.
En el caso de rasante
entre alas y alma combinado con flexión transversal, se calcularán las armaduras
necesarias por ambos conceptos y se dispondrá la mayor de las dos.
Figura 44.2.3.5.b
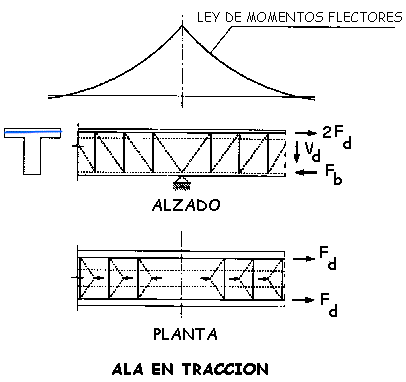
Figura 44.2.3.5.c
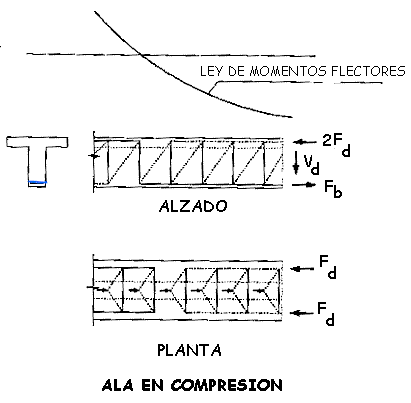
Nota de www.carreteras .org: estas dos figuras no se publicaron en los
boletines oficiales del estado, las hemos tomado de la publicación del servicio de
publicaciones del Ministerio de Fomento.




