Las prescripciones incluidas en este artículo son de aplicación exclusivamente a elementos lineales sometidos a torsión pura o a esfuerzos combinados de torsión y flexión, cortante y axil.

A los efectos de este artículo se consideran elementos lineales aquellos cuya distancia entre puntos de momento nulo es igual o superior a dos veces y media su canto total y cuya anchura es igual o inferior a cuatro veces dicho canto, pudiendo ser su directriz recta o curva.

Los estados de flexión bidimensional (m_x, m_y y m_xy) en losas o placas se dimensionarán de acuerdo con el Artículo 42.º, teniendo en cuenta las direcciones principales de los esfuerzos y las direcciones en que se disponga la armadura.

Cuando el equilibrio estático de una estructura dependa de la resistencia a torsión de uno o varios de los elementos de la misma, éstos deberán ser dimensionados y comprobados de acuerdo con el presente artículo. Cuando el equilibrio estático de la estructura no depende de la resistencia a torsión de uno o varios de los elementos de la misma sólo será necesario comprobar este Estado Límite en aquellos elementos cuya rigidez a torsión haya sido considerada en el cálculo de esfuerzos.

Para evitar una excesiva fisuración en piezas lineales, deberán disponerse las armaduras mínimas indicadas en el Artículo 49.º

La resistencia a torsión de las secciones se calcula utilizando una sección cerrada de pared delgada. Así, las secciones macizas se sustituyen por secciones equivalentes de pared delgada. Las secciones de forma compleja, como secciones en T, se dividen en varias subsecciones, cada una de las cuales se modeliza como una sección equivalente de pared delgada y la resistencia total a torsión se calcula como la suma de las capacidades de las diferentes piezas. La división de la sección debe ser tal que maximice la rigidez calculada. En zonas cercanas a los apoyos no podrán considerarse como colaborantes a la rigidez a torsión de la sección aquellos elementos de la misma cuya transmisión de esfuerzos a los elementos de apoyo no pueda realizarse de forma directa.

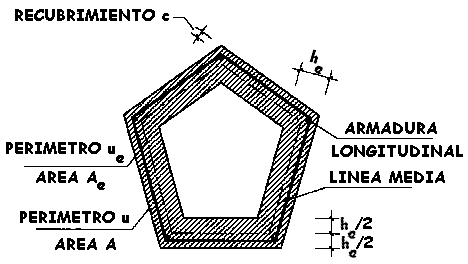
El espesor eficaz h_e de la pared de la sección de cálculo (figura 45.2.1) será:

• h_e £ A/u
  • no mayor de h₀
  • no menor de 2c

Puede utilizarse un valor de h_e inferior a A/u, siempre que cumpla con las condiciones mínimas expresadas y que permita satisfacer las exigencias de compresión del hormigón establecidas en 45.2.2.1.

El Estado Límite de Agotamiento por torsión puede alcanzarse, ya sea por agotarse la resistencia a compresión del hormigón o por agotarse la resistencia a tracción de las armaduras dispuestas. En consecuencia, es necesario comprobar que se cumple simultáneamente:

• T_d £ T_u1
• T_d £ T_u2
• T_d £ T_u3

Las armaduras de torsión se suponen constituidas por una armadura transversal formada por cercos cerrados situados en planos normales a la directriz de la pieza. La armadura longitudinal estará constituida por armadura pasiva o activa paralela a la directriz de la pieza, distribuida uniformemente con separaciones no superiores a 30 cm en el contorno exterior de la sección hueca eficaz o en una doble capa en el contorno exterior y en el interior de la sección hueca eficaz o real. Al menos se situará una barra longitudinal en cada esquina de la sección real para asegurar la transmisión a la armadura transversal de las fuerzas longitudinales ejercidas por las bielas de compresión. 

El esfuerzo torsor de agotamiento que pueden resistir las bielas comprimidas se deduce de la siguiente expresión:

T_u1=af_1cdA_eh_e [cotgq/(1+cotg²q)]

•  f_1cd Resistencia a compresión del hormigón. f_1cd=0,60f_cd
• a
  • 1,20 si hay estribos únicamente a lo largo del perímetro exterior de la pieza;
  • 1,50 si se colocan estribos cerrados en ambas caras de la pared de la sección hueca equivalente o de la sección hueca real.
• q Angulo entre las bielas de compresión de hormigón y el eje de la pieza. Se adoptará un valor que cumpla: 0,4 £ cotgq £ 2,5
• A_e Área encerrada por la línea media de la sección hueca eficaz de cálculo (figura 45.2.1).

El esfuerzo torsor que pueden resistir las armaduras transversales viene dado por:

• A_t Área de las armaduras utilizadas como cercos o armadura transversal.
• s_t Separación longitudinal entre cercos o barras de la armadura transversal.
• f_yt,d Resistencia de cálculo del acero de la armadura A_t (40.2).
  • Para armaduras pasivas f_yt,d=s_sd
  • Para armaduras activas f_yt,d=s_pd

El esfuerzo torsor que pueden resistir las armaduras longitudinales se puede calcular mediante:

•  A_l Área de las armaduras longitudinales.
• f_yl,d Resistencia de cálculo del acero de la armadura longitudinal A_l, (40.2).
  • Para armaduras pasivas f_yl,d=s_sd
  • Para armaduras activas f_yl,d=s_pd
• u_e Perímetro de la línea media de la sección hueca eficaz de cálculo A_e (figura 45.2.1).

En general pueden ignorarse en el cálculo de las piezas lineales de hormigón las tensiones producidas por la coacción del alabeo torsional. 

La separación longitudinal entre cercos de torsión s_t no excederá de

 s_t £ u_e/8

• s_t £ 0,80a,  no mayor de 300 mm  si T_d£1/5T_u1
• s_t £ 0,60a,  no mayor de 300 mm  si 1/5T_u1<T_d£2/3T_u1
• s_t £ 0,30a,  no mayor de 200 mm  si T_d>2/3T_u1

Se utilizará el mismo procedimiento que en torsión pura (45.2.1) para definir una sección hueca eficaz de cálculo. Las tensiones normales y tangenciales producidas por los esfuerzos actuantes sobre esta sección se calculan a través de los métodos elásticos o plásticos convencionales.

Una vez halladas las tensiones, las armaduras necesarias en cualquier pared de la sección hueca eficaz de cálculo pueden determinarse mediante las fórmulas de distribución de tensión plana. También puede determinarse la tensión principal de compresión en el hormigón. Si las armaduras deducidas de este modo no fueran factibles o convenientes, pueden cambiarse en alguna zona las tensiones deducidas por un sistema de fuerzas estáticamente equivalentes y emplear éstas en el armado. Deberán, en este caso, comprobarse las consecuencias que dicho cambio provoca en las zonas singulares como huecos o extremos de las vigas.

Las tensiones principales de compresión s_cd deducidas en el hormigón, en las distintas paredes de la sección hueca eficaz de cálculo, deben cumplir:

s_cd £ af_1cd

donde a y f_1cd son los definidos  en 45.2.2.1. y 40.3 respectvamente.

Las armaduras longitudinales necesarias para torsión y flexocompresión o flexotracción se calcularán por separado suponiendo la actuación de ambos tipos de esfuerzo de forma independiente. Las armaduras así calculadas se combinarán de acuerdo con las siguientes reglas:

•  a) En la zona traccionada debida a la flexión compuesta, las armaduras longitudinales por torsión se sumarán a las necesarias por flexión y esfuerzo axil.
• b) En la zona comprimida debido a la flexión compuesta, si la capacidad mecánica de las armaduras de torsión a disponer es inferior al esfuerzo de compresión del hormigón debido a la flexión compuesta, no será necesario añadir armadura por torsión. En caso contrario se añadirá la diferencia entre ambos valores.

Por lo que respecta a las compresiones en el hormigón, deberá comprobarse que la tensión principal de compresión s_cd en el punto crítico de la sección cumple:

s_cd £ af_1cd

Para la determinación de s_cd se empleará la tensión de compresión s_md debida a la flexión compuesta en el punto considerado y la tensión tangencial de torsión en dicho punto calculada de acuerdo con:

t_td = T_d / (2A_eh_e) 

s_cd = s_md/2 + [(s_md/2)²+t²_td]^1/2

Los esfuerzos torsores y cortantes de cálculo concomitantes deberán satisfacer la siguiente condición para asegurar que no se producen compresiones excesivas en el hormigón:

(T_d/T_u1)^b+(V_rd/V_u1)^b £ 1

b=2(1-h_e/b)

•  b Anchura del elemento, igual a la anchura total para sección maciza y a la suma de las anchuras de las almas para sección cajón.

Los cálculos para el dimensionamiento de los estribos se realizarán de forma independiente, para la torsión de acuerdo con 45.2.2.2 y para el cortante con 44.2.3.2.2. En ambos cálculos se utilizará el mismo ángulo q para las bielas de compresión. Las armaduras así calculadas se sumarán teniendo en cuenta que las de torsión deben disponerse en el perímetro exterior de la sección, lo cual no es preceptivo con las de cortante.