Se entiende por pretensado la aplicación controlada de una tensión al hormigón mediante el tesado de tendones de acero. Los tendones serán de acero de alta resistencia y pueden estar constituidos por alambres, cordones o barras.

En esta Instrucción no se consideran otras formas de pretensado.

De acuerdo con la situación del tendón respecto de la sección transversal, el pretensado puede ser:

• a) Interior. En este caso el tendón está situado en el interior de la sección transversal de hormigón.
• b) Exterior. En este caso el tendón está situado fuera del hormigón de la sección transversal y dentro del canto de la misma.

De acuerdo con el momento del tesado respecto del hormigonado del elemento, el pretensado puede ser:

• a) Con armaduras pretesas. El hormigonado se efectúa después de haber tesado y anclado provisionalmente las armaduras en elementos fijos. Cuando el hormigón ha adquirido suficiente resistencia, se liberan las armaduras de sus anclajes provisionales y, por adherencia, se transfiere al hormigón la fuerza previamente introducida en las armaduras.
• b) Con armaduras postesas. El hormigonado se realiza antes del tesado de las armaduras activas que normalmente se alojan en conductos o vainas. Cuando el hormigón ha adquirido suficiente resistencia se procede al tesado y anclaje de las armaduras.

Desde el punto de vista de las condiciones de adherencia del tendón, el pretensado puede ser:

•  a) Adherente. Este es el caso del pretensado con armadura pretesa o con armadura postesa en el que después del tesado se procede a ejecutar una inyección con un material que proporciona una adherencia adecuada entre la armadura y el hormigón del elemento (Artículo 36.2).
• b) No adherente. Este es el caso del pretensado con armadura postesa en el que se utilizan como sistemas de protección de las armaduras, inyecciones que no crean adherencia entre ésta y el hormigón del elemento (Artículo 36.3).

La fuerza de tesado P_o ha de proporcionar sobre las armaduras activas una tensión s_p0 no mayor, en cualquier punto, que el menor de los dos valores siguientes:

• 0,75 f_pmaxk
• 090 f_pk

De forma temporal, esta tensión podrá aumentarse hasta el menor de los valores siguientes:

• 0,85 f_pmaxk
• 095 f_pk

Las pérdidas instantáneas de fuerza son aquellas que pueden producirse durante la operación de tesado y en el momento del anclaje de las armaduras activas y dependen de las características del elemento estructural en estudio. Su valor en cada sección es:

DP_i = DP₁ + DP₂ + DP₃

• DP₁ Pérdidas de fuerza, en la sección en estudio, por rozamiento a lo largo del conducto de pretensado.
• DP₂ Pérdidas de fuerza, en la sección en estudio, por penetración de cuñas en los anclajes.
• DP₃ Pérdidas de fuerza, en la sección en estudio, por acortamiento elástico del hormigón.

Las pérdidas teóricas de fuerza por rozamiento entre las armaduras y las vainas o conductos de pretensado, dependen de la variación angular total a, del trazado del tendón entre la sección considerada y el anclaje activo que condiciona la tensión en tal sección; de la distancia x entre estas dos secciones; del coeficiente m de rozamiento en curva y del coeficiente K de rozamiento en recta, o rozamiento parásito. Estas pérdidas se valorarán a partir de la fuerza de tesado P₀.

Las pérdidas por rozamiento en cada sección pueden evaluarse mediante la expresión:

 DP₁ = P₀[1-e^-(ma+Kx)]

• m Coeficiente de rozamiento en curva.
• a Suma de los valores absolutos de las variaciones angulares (desviaciones sucesivas), medidas en radianes, que describe el tendón en la distancia x. Debe recordarse que el trazado de los tendones puede ser una curva alabeada debiendo entonces evaluarse a en el espacio.
• K Coeficiente de rozamiento parásito, por metro lineal.
• x Distancia, en metros, entre la sección considerada y el anclaje activo que condiciona la tensión en la misma (ver figura 20.2.2.1.1).

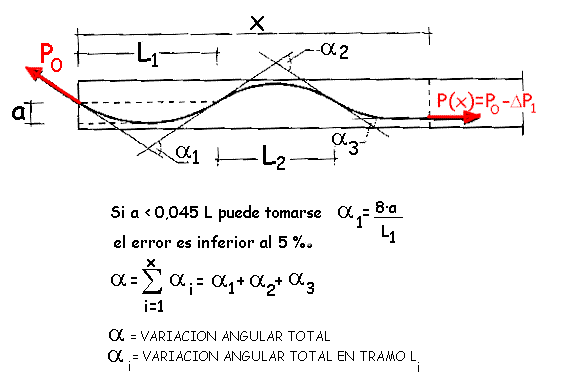
Los datos correspondientes a los valores de m y de K deben definirse experimentalmente, habida cuenta del procedimiento de pretensado utilizado. A falta de datos concretos pueden utilizarse los valores experimentales sancionados por la práctica.

En tendones rectos postesos de corta longitud, la pérdida de fuerza por penetración de cuñas, DP₂ puede deducirse mediante la expresión:

DP₂=(a/L)·E_pA_p

En los demás casos de tendones rectos, y en todos los casos de trazados curvos, la valoración de la pérdida de tensión por penetración de cuñas se hará teniendo en cuenta los rozamientos en los conductos. Para ello podrán considerarse las posibles variaciones de m y de K al destesar el tendón, respecto a los valores que aparecen al tesar.

En el caso de armaduras constituidas por varios tendones que se van tesando sucesivamente, al tesar cada tendón se produce un nuevo acortamiento elástico del hormigón que descarga, en la parte proporcional correspondiente a este acortamiento, a los anteriormente anclados.

Cuando las tensiones de compresión al nivel del baricentro de la armadura activa en fase de tesado sean apreciables, el valor de estas pérdidas, DP₃, se podrá calcular, silos tendones se tesan sucesivamente en una sola operación, admitiendo que todos los tendones experimentan un acortamiento uniforme, función del número n de los mismos que se tesan sucesivamente, mediante la expresión:

 DP₃=s_cp·[(n-1)/2n]·(E_pA_p/E_cj)

• A_p Sección total de la armadura activa.
• s_cp Tensión de compresión, a nivel del centro de gravedad de las armaduras activas, producida por la fuerza P₀-DP₁-DP₂ y los esfuerzos debidos a las acciones actuantes en el momento del tesado.
• E_p Módulo de deformación longitudinal de las armaduras activas.
• E_cj Módulo de deformación longitudinal del hormigón para la edad j correspondiente al momento de la puesta en carga de las armaduras activas.

Se denominan pérdidas diferidas a las que se producen a lo largo del tiempo, después de ancladas las armaduras activas. Estas pérdidas se deben esencialmente al acortamiento del hormigón por retracción y fluencia y a la relajación del acero de tales armaduras.

La fluencia del hormigón y la relajación del acero están influenciadas por las propias pérdidas y, por lo tanto, resulta imprescindible considerar este efecto interactivo.

Siempre que no se realice un estudio más detallado de la interacción de estos fenómenos, las pérdidas diferidas pueden evaluarse de forma aproximada de acuerdo con la expresión siguiente:

DP_dif={[n·j(t,t₀)·s_cp+E_p·e_cs(t,t₀)+0,80·Ds_pr]·A_p}/{1+[n·(A_p/A_c)·[1+(A_c·Y²_p/I_c)·(1+c,j(t,t₀)]]}

• Y_p Distancia del centro de gravedad de las armaduras activas al centro de gravedad de la sección.
• n Coeficiente de equivalencia = E_p/E_c.
• j(t,t₀) Coeficiente de fluencia para una edad de puesta en carga igual a la edad del hormigón en el momento del tesado (t₀) (ver 39.8).
• e_cs Deformación de retracción que se desarrolla tras la operación de tesado (ver 39.7).
• s_cp Tensión en el hormigón en la fibra correspondiente al centro de gravedad de las armaduras activas debida a la acción del pretensado, el peso propio y la carga muerta.
• Ds_pr Pérdida por relajación a longitud constante. Puede evaluarse utilizando la siguiente expresión:  Ds_pr=r_f·(P_ki/A_p) siendo r_f el valor de la relajación a longitud constante a tiempo infinito (ver 38.9) y A_p el área total de las armaduras activas. P_ki es el valor característico de la fuerza inicial de pretensado, descontadas las pérdidas instantáneas.
• A_c Area de la sección de hormigón.
• I_c Inercia de la sección de hormigón.
• c Coeficiente de envejecimiento. Simplificadamente, y para evaluaciones a tiempo infinito, podrá adoptarse c = 0,80.

Para armaduras pretesas, las pérdidas a considerar desde el momento de tesar hasta la transferencia de la fuerza de tesado al hormigón son:

• a) Penetración de cuñas.
• b) Relajación a temperatura ambiente hasta la transferencia.
• c) Relajación adicional de la armadura debida, en su caso, al proceso de calefacción.
• d) Dilatación térmica de la armadura debida, en su caso, al proceso de calefacción.
• e) Retracción anterior a la transferencia.
• f) Acortamiento elástico instantáneo al transferir.

Las pérdidas diferidas posteriores a la transferencia se obtendrán de igual forma que en armaduras postesas, utilizando los valores de retracción y relajación que se producen después de la transferencia.

Los efectos estructurales del pretensado pueden representarse utilizando tanto un conjunto de fuerzas equivalentes autoequilibradas, como un conjunto de deformaciones impuestas. Ambos métodos conducen a los mismos resultados.

El sistema de fuerzas equivalentes se obtiene del equilibrio del cable y está formado por:

• Fuerzas y momentos concentrados en los anclajes.
• Fuerzas normales a los tendones, resultantes de la curvatura y cambios de dirección de los mismos.
• Fuerzas tangenciales debidas al rozamiento.

El valor de las fuerzas y momentos concentrados en los anclajes se deduce del valor de la fuerza de pretensado en dichos puntos, calculada de acuerdo con el apartado 20.2, de la geometría del cable, y de la geometría de la zona de anclajes (ver figura 20.3.1).

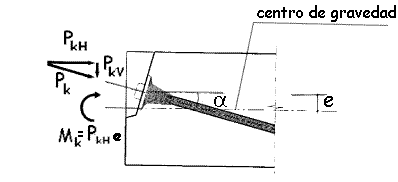
Para el caso específico de vigas, con simetría respecto a un plano vertical, en el anclaje existirá una componente horizontal y otra vertical de la fuerza de pretensado y un momento flector, cuyas expresiones vendrán dadas por:

• P_k,H=P_kcosa
• P_k,V=P_ksena
• M_k=P_k,H·e

• a Ángulo que forma el trazado del pretensado respecto de la directriz del elemento, en el anclaje.
• P_k Fuerza en el tendón según 20.2.
• e Excentricidad del tendón respecto del centro de gravedad de la sección.

Las fuerzas normales distribuidas a lo largo del tendón, n(x), son función de la fuerza de pretensado y de la curvatura del tendón en cada punto, 1/r(x). Las fuerzas tangenciales, t(x), son proporcionales a las normales a través del coeficiente de rozamiento m, según:

n(x)= P_k(x)/r(x) ; t(x)=-m·n(x)

Alternativamente, en el caso de elementos lineales, los efectos estructurales del pretensado se pueden introducir mediante la aplicación de deformaciones y curvaturas impuestas que, en cada sección, vendrán dadas por:

e_p=P_k/(E_cA_c)

Los esfuerzos estructurales debidos al pretensado tradicionalmente se definen distinguiendo entre:

• Esfuerzos isostáticos
• Esfuerzos hiperestáticos

Los esfuerzos isostáticos dependen de la fuerza de pretensado y de la excentricidad del pretensado respecto del centro de gravedad de la sección, y pueden analizarse a nivel de sección. Los esfuerzos hiperestáticos dependen, en general, del trazado del pretensado, de las condiciones de rigidez y de las condiciones de apoyo de la estructura y deben analizarse a nivel de estructura.

La suma de los esfuerzos isostático e hiperestático de pretensado es igual a los esfuerzos totales producidos por el pretensado.

Cuando se compruebe el Estado Límite de Agotamiento frente a solicitaciones normales de secciones con armadura adherente, de acuerdo con los criterios expuestos en el artículo 42.º, los esfuerzos de cálculo deben incluir la parte hiperestática del efecto estructural del pretensado considerando su valor de acuerdo con los criterios del apartado 13.2. La parte isostática del pretensado se considera, al evaluar la capacidad resistente de la sección, teniendo en cuenta la predeformación correspondiente en la armadura activa adherente.